Vektorrechnung Punkte auf Geraden angeben und weitere Geradengleichung aufstellen YouTube

Punktprobe Gerade:In dem heutigen Video geht es darum, wie du rechnerisch überprüfen kannst, ob ein gegebener Punkt auf einer Geraden liegt oder eben nicht..
Lernvoraussetzungen 2Punkteform der Geradengleichung. SMultiplikation.Überprüfen, ob ein Punkt

Dieser Überblick fasst das Wichtigste nochmals zusammen. Schritt 1: Wir setzten den gegebenen Punkt in die Geradengleichung ein. Schritt 2: Wir überprüfen, ob wir ein wahres Ergebnis erhalten. Schritt 3: Erhalten wir eine wahre Aussage → Punkt liegt auf der Geraden. Erhalten wir ein falsches Ergebnis → Punkt liegt nicht auf der Geraden.
Vektoren Grundlagen zu Vektoren leicht erklärt

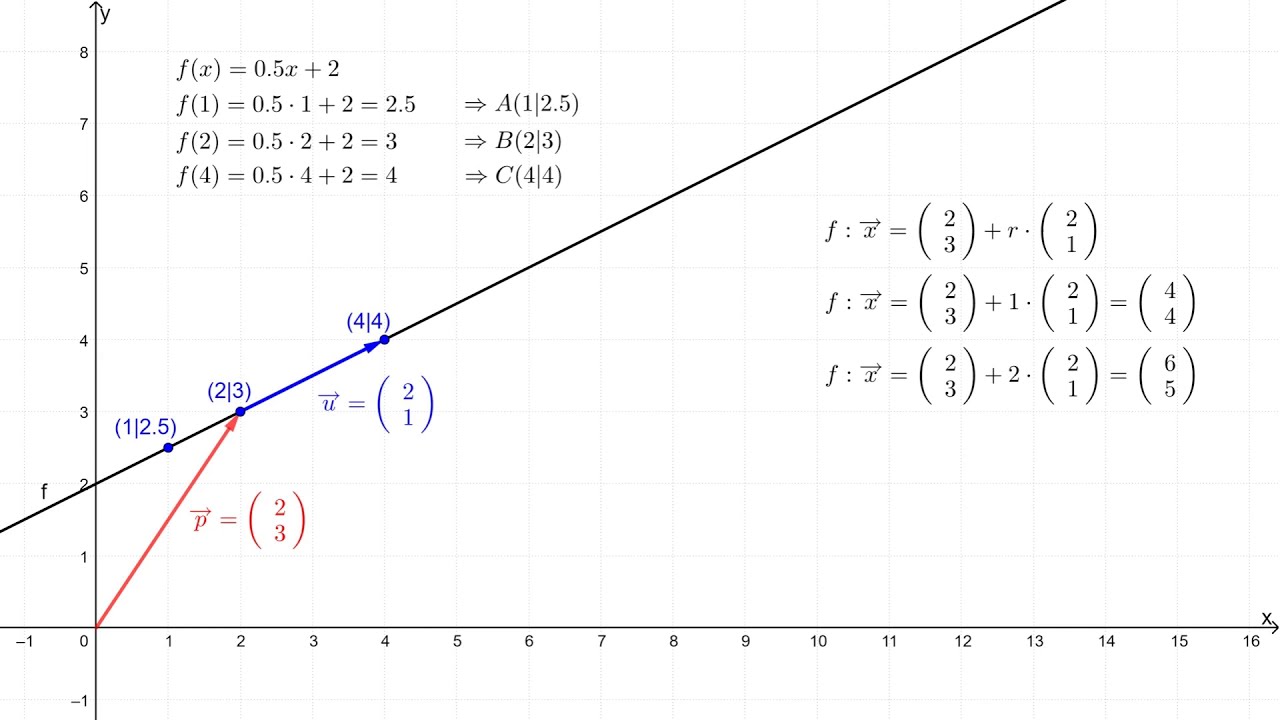
Vorgehensweise. Punkt P P auf Strecke \overline {AB} AB? Aus A A und B B die Geradengleichung aufstellen. Punktprobe mit P P auf g_ {AB} gAB. r r muss zwischen 0 und 1 liegen*. *Voraussetzung ist, dass die Geradengleichung \vec {x} = \vec {OA} + r \cdot \vec {AB} x = OA+r ⋅ AB lautet (keinen anderen Stütz- oder Richtungsvektor).
Überprüfen sie rechnerisch, ob der Punkt P (35) auf dem Graphen der Funktion g(x) liegt
Beispiel. Eine Gerade wird zum Beispiel durch die Koordinatenform. dargestellt. Möchtest du nun überprüfen, ob ein Punkt auf der Gerade liegt, dann setzt du lediglich die Komponenten des Punktes in die Form ein und schaust, ob die Gleichung erfüllt wird.. So liegt zum Beispiel der Punkt auf der Gerade , denn. Der Punkt hingegen liegt nicht auf der Gerade, da
Pin auf Lineare Funktionen (Geraden)

Sie suchen eine Karte oder den Stadtplan von Sydney und Umgebung? Finden Sie auf der Karte von Sydney eine gesuchte Adresse, berechnen Sie die Route von oder nach Sydney oder lassen Sie sich alle Sehenswürdigkeiten und Restaurants aus dem Guide Michelin in oder um Sydney anzeigen. Der ViaMichelin-Stadtplan von Sydney: Nutzen Sie die bewährten.
Beschreibung einer Geraden mit Vektoren GeoGebra

Bei dieser Formel steht für einen Vektor, der auf jeden beliebigen Punkt auf der Geraden zeigt - je nachdem was man im rechten Teil der Gleichung für einsetzt. Will man nun herausfinden, ob ein Punkt auf einer bestimmten Geraden liegt, so bietet es sich an, diesen Punkt einfach für einzusetzen. Kann man dann ein finden, durch welches sich genau dieser Punkt ergibt, so liegt er auf der Geraden.
Punkte berechnen, die auf einer Gerade (mit gegebener Parametergleichung) liegen YouTube
13 Punkte auf der Geraden. Um Punkte zu erhalten, die auf der Geraden liegen, musst du Werte für \lambda λ einsetzen. So kannst du mit dem passenden Wert jeden Punkt auf der Gerade erhalten. Wenn du überprüfen willst, ob ein Punkt auf der Geraden liegt musst du zunächst den Punkt mit der Geradengleichung gleichsetzen.
Liegt der Punkt auf der Geraden Punktprobe lineare Funktionen Geraden Übungen mit

Geraden Punktprobe. Um zu überprüfen, ob ein gegebener Punkt A auf einer Geraden g liegt, führt man eine Punktprobe durch. Dazu setzt man den Ortsvektor → O A des gegebenen Punktes für → x in die Parametergleichung g: → x = → p + s ⋅ → u; s ∈ R der Geraden ein. Anschließend löst man zeilenweise nach dem Parameter s auf.. Dann gibt es zwei Möglichkeiten:
Punktprobe; liegt ein Punkt auf dem Graphen einer Funktion YouTube

Punktprobe Gerade in Normalenform. Überprüfe, ob der Punkt auf der Geraden liegt! Schritt 1: Punkt in Gerade einsetzen. Schritt 2: Gleichung bzw. Gleichungssystem lösen. Schritt 3: Lösung interpretieren. Die Gleichung hat keine Lösung. Demzufolge liegt der Punkt nicht auf der Geraden.
Liegt der PUNKT auf der GERADEN? PUNKTPROBE Übungen mit Lösungen lineare Funktion

Ein Foto auf den Stufen vor dem weltweit bekannten Sydney Opera House schießen.; Von der Harbour Bridge die fantastische Aussicht über den Port Jackson genießen.; Einen Spaziergang durch die eindrucksvollen Royal Botanic Gardens unternehmen.; An einem Harbour Cruise teilnehmen und durch die lebendigen Gewässer schippern.; Im spannenden Stadtteil Kings Cross ausgehen & einen Nachtclub besuchen.
PunktRichtungsform einer Geraden GeoGebra

Punktprobe Vektoren. PDF. Word. Möchtest du testen, ob ein Punkt auf einer gegebenen Geraden liegt, so kannst du eine Punktprobe durchführen. Dabei setzt du den Ortsvektor des Punktes mit der Geradengleichung zu gleich. Dadurch erhältst du ein lineares Gleichungssystem und kannst überprüfen, ob es einen möglichen Parameterwert für gibt.
Punktprobe Gerade Um zu überprüfen, ob ein Punkt auf einer Geraden liegt, muss der

Punktprobe mit Gerade (Vektoren):In dem heutigen Video spreche ich mit dir darüber, wie man überprüft, ob ein gegebener Punkt auf einer vektoriellen Geraden.
B4 Ich kann überprüfen, ob ein Punkt in einer Strecke liegt YouTube

Parameterform einer Geraden ist die Punktprobe. Damit prüft man, ob ein Punkt auf einer Geraden liegt. Wir sehen diese uns im Artikel Punktprobe bei Vektoren an. Anzeige:. Der Punkt hat damit eine x-Angabe, eine y-Angabe und eine z-Angabe. Auch der Vektor wird um ein z erweitert. Im nächsten Koordinatensystem sieht man eine Gerade zwischen.
Geraden Geradengleichung, Punkte einer Geraden und Punktprobe YouTube

Fazit. Da in jeder Zeile des Gleichungssystems denselben Wert annimmt, befindet sich der Punkt auf der Gerade. Beispiel 2. Gegeben ist eine Geradengleichung in Parameterform. Überprüfe, ob der Punkt auf der Gerade liegt. Punkt für in die Geradengleichung einsetzen. Gleichungssystem aufstellen. zeilenweise berechnen. Fazit.
Überprüfen Sie, ob die Punkte auf einer Geraden liegen. Mathelounge
Die Spanfläche A γ ist die Fläche der Schneide, auf der der Span abläuft. Die Freifläche A α ist die Fläche am Schneidkeil, die der neu entstehenden Werkstückoberfläche, der Schnittfläche, zugekehrt ist. Diese Bezeichnungen verdeutlichen, dass der Schneidkeil (Werkzeug) immer in Beziehung zum Werkstück zu betrachten ist, was bedeutet, dass der Verfahrenskinematik eine erhebliche.
Mathe 7 Punktprobe (Liegt ein Punkt auf der Geraden?) YouTube

1. Um zu überprüfen ob dieser Punkt auf der Geraden liegt, setzt ihr diesen in die Gerade ein: 2. Löst die Gleichung zeilenweise. Kommt in jeder Zeile dasselbe Ergebnis raus, liegt der Punkt auf der Geraden: Wie ihr seht, liegt dieser Punkt nicht auf der Geraden, da in der 3. Zeile ein anderer Wert als in den ersten beiden raus kommt.