Analysis 1 Stetige Funktionen EpsilonDeltaDefinition / εδKriterium d. Stetigkeit (Lektion

Mathematisch: Eine Funktion ist an einer Stelle x 0 stetig, wenn für den Grenzwert ( Limes, kurz lim) gilt: limx→x0 f(x) = f(x0) lim x → x 0 f ( x) = f ( x 0) Eine Funktion ist insgesamt stetig (nicht nur an einer bestimmten Stelle x 0 ), wenn das für jedes beliebige x 0 aus dem Definitionsbereich der Funktion gilt.
Stetigkeit Nachhilfe von Tatjana Karrer

Definition. Eine Funktion f ( x) ist an einer Stelle x 0 stetig, wenn. [ 1] f ( x 0) definiert ist. [ 2] lim x → x 0 f ( x) existiert. [ 3] lim x → x 0 f ( x) = f ( x 0) zu [1] Wenn f in x 0 nicht definiert ist, so ist es sinnlos zu fragen, ob f in x 0 stetig ist. Beispiel 1.
Wann ist eine Funktion "stetig und differenzierbar"? (Schule, Mathematik, Studium)
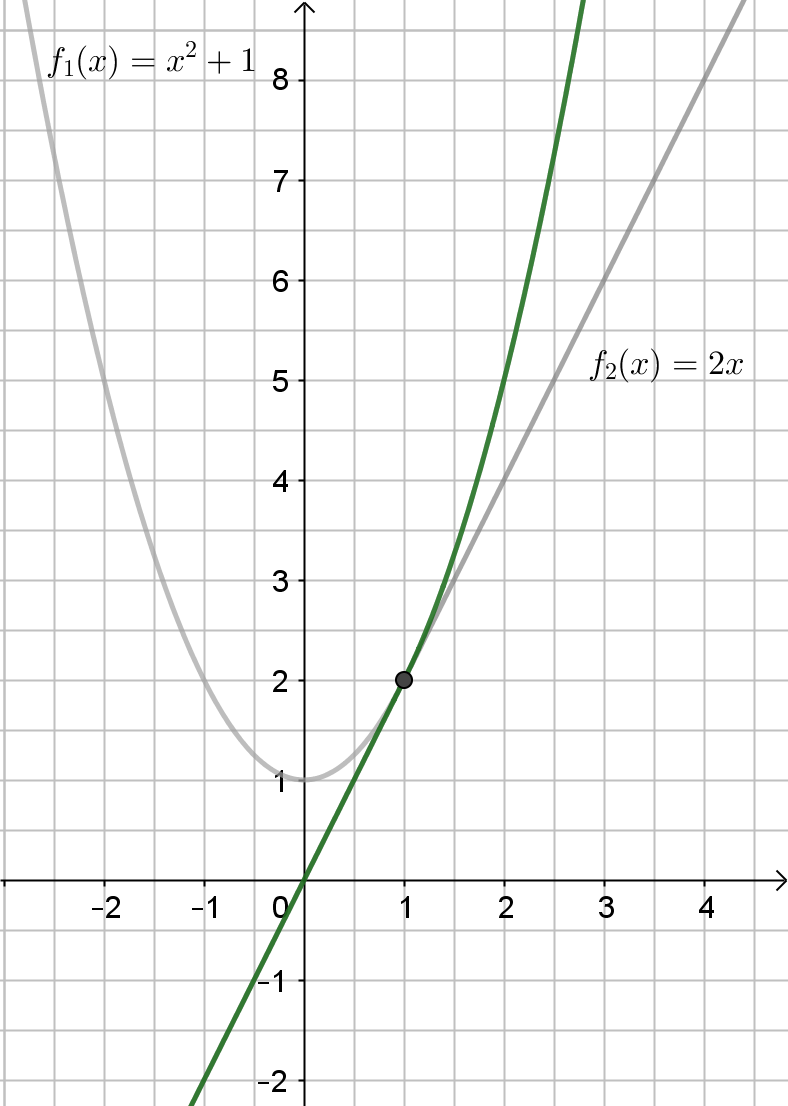
Stetigkeit Definition. Eine Funktion f (x) heißt dann in einem Intervall [ a ; b ] stetig, wenn man den dazugehörigen Graphen von einem Intervallpunkt bis zum anderen zeichnen kann, ohne den Stift dabei absetzen zu müssen. oder.
Mathe Klasse 7 / Wann ist eine Funktion eine Funktion? YouTube

Wenn du x = -1 in die Funktion g (x) einsetzt, erhältst du den Funktionswert g (-1) = 1. Dein beidseitiger Grenzwert ist ebenfalls gleich 1. g (x) ist an der Stelle x = -1 also stetig .Tatsächlich handelt es sich bei der Funktion g (x) = x 2 um eine stetige Funktion.
Stetigkeit und Zwischenwertsatz online lernen

Eine Funktion f (x), die in der Umgebung von x 0 definiert ist, heißt an einer Stelle x 0 des Definitionsbereichs stetig, wenn sie einen eindeutigen Grenzwert für x gegen x 0 besitzt und wenn Grenzwert und Funktionswert an dieser Stelle gleich groß sind.
Stetigkeit einer Funktion OnlineKurse
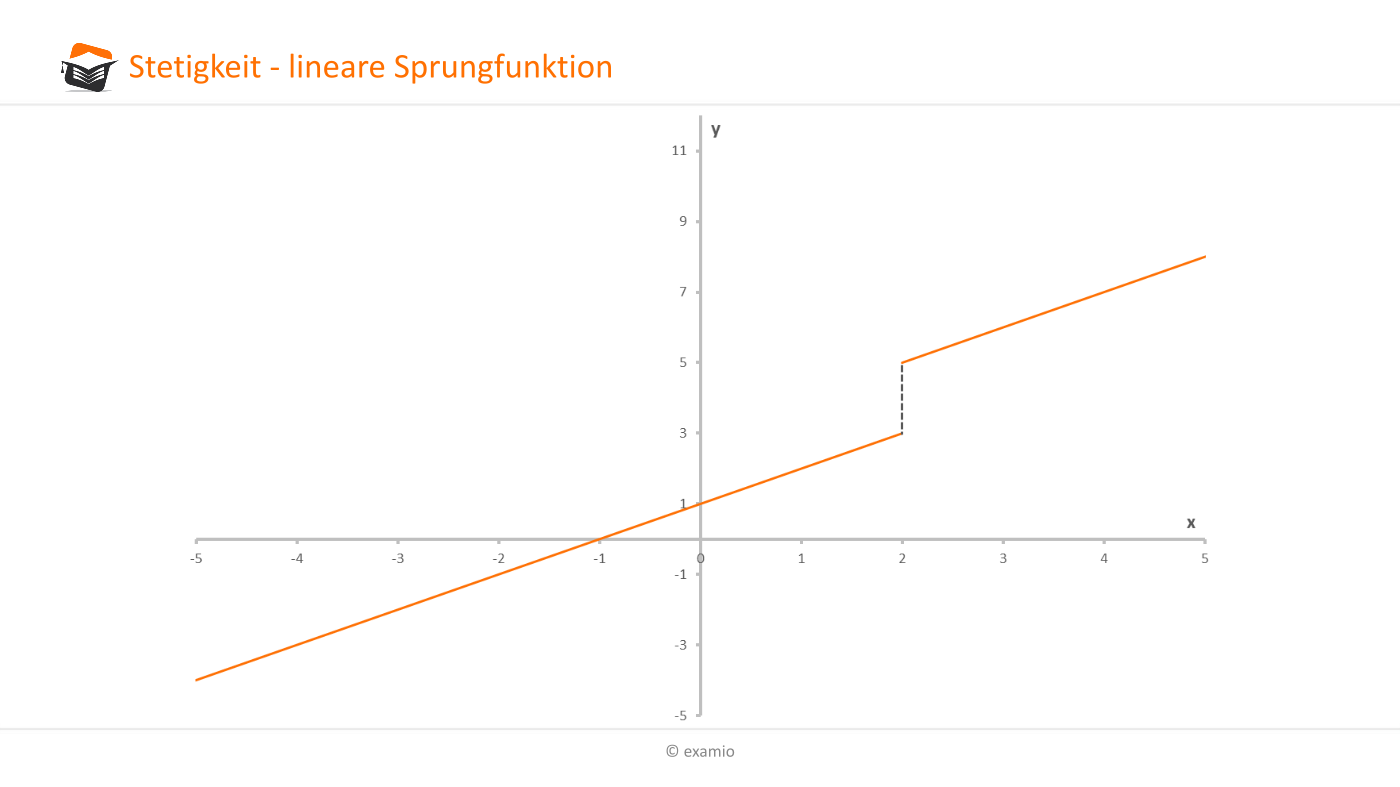
Die Definition von Stetigkeit nach Heine besagt, dass eine Funktion an einer Stelle x0 stetig ist, wenn zu jeder noch so kleinen positiven Zahl ε ein positives δ existiert, so dass für alle x, die in der δ-Umgebung der Stelle x0 liegen (außer x0 selbst), der Funktionswert f (x) in der ε-Umgebung von f (x0) liegt. 3.
www.mathefragen.de Wie beweise ich dass eine Funktion nicht gleichmässig stetig ist?

Mathematisch gesehen, wird Stetigkeit mithilfe des Grenzwerts definiert: Merke: Eine Funktion f ( x) ist an der Stelle a stetig wenn gilt: Gründe für Unstetigkeit. Es gibt drei Gründe, weshalb eine Funktion f ( x) an einer Stelle c nicht stetig ist. Ein weißer Punkt gibt an, dass die Funktion an dieser Stelle nicht definiert ist.
Definitionsbereich bzw. Definitionsmenge einer Funktion ermitteln
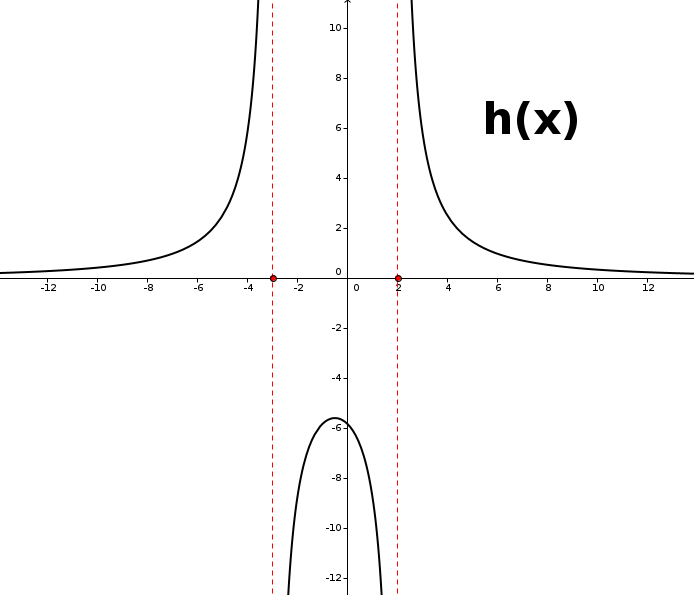
Stetigkeit. Eine Funktion f f heißt genau dann stetig an einer Stelle x_0 x0, wenn der Funktionswert an dieser Stelle mit sowohl dem links- als auch rechtsseitigem Grenzwert identisch ist, d.h. wenn gilt: f (x_0)=\lim_ {x\rightarrow x_0^-}f (x)=\lim_ {x\rightarrow x_0^+}f (x) f (x0) = limx→x0− f (x) = limx→x0+ f (x)
www.mathefragen.de Wie beweise ich ob eine Funktion stetig ist?

Eine Funktion ist an der Stelle x 0 dann stetig, wenn an dieser Stelle der Funktionswert mit dem Grenzwert übereinstimmt. Eine Funktion, die an jeder Stelle ihres Definitionsbereichs stetig ist, heißt stetige Funktion. lim x → x 0. f ( x) = f ( x 0)
PPT Hands on Mathematik Stetigkeit & Differenzierbarkeit PowerPoint Presentation ID1302972
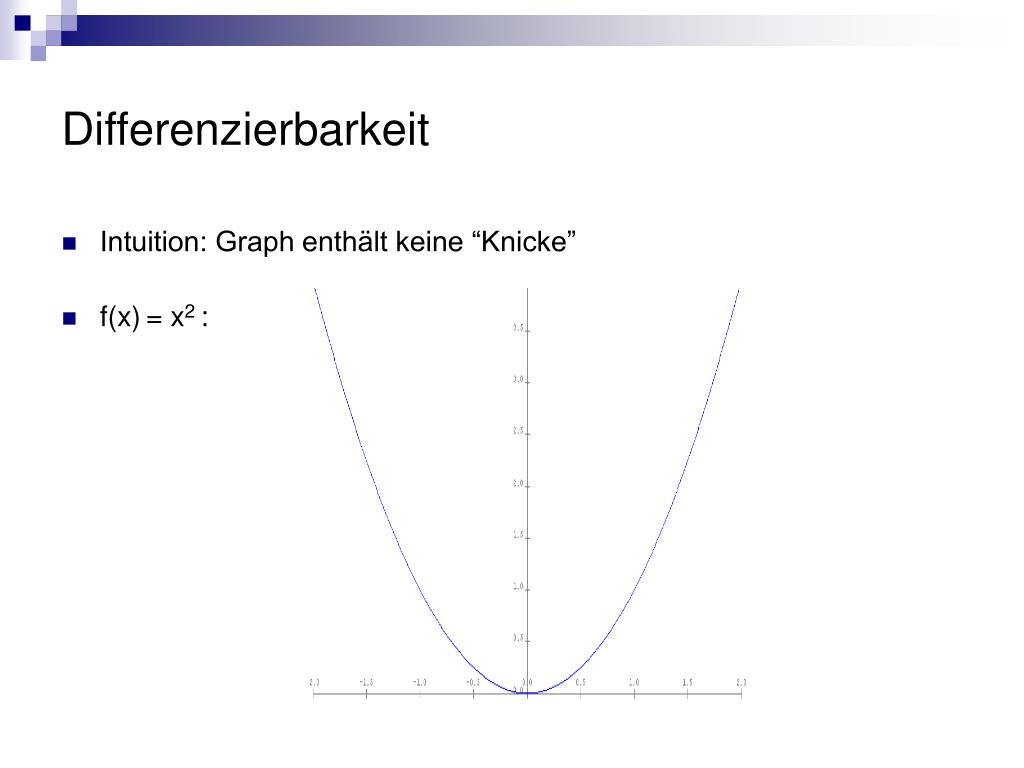
Stetigkeit. intuitiv. reelle Funktionen. Funktions- darstellungen. Der Definitionsbereich ist hier die ganze Menge \mathbb {R} . Da aber grundsätzlich keine Einschränkung an die Zuordnungsvorschrift, die eine Funktion definiert, gemacht werden, gibt es zahlreiche andere Funktionen, die nicht auf eine solch einfache Weise festgelegt werden können.
Abschnittsweise definierte Funktionen Stetigkeit & Differenzierbarkeit. Ist die Aufgabe richtig
Wenn wir Funktionswerte annähern, nutzen wir das Konzept der Stetigkeit (auch wenn wir uns dessen nicht bewusst sind). Anstatt zu bestimmen, kann auch die Annäherung verwendet werden, wenn hinreichend nah an liegt. Diese Approximation ist jedoch nur dann sinnvoll, wenn die Funktion an der Stelle stetig ist.
Stetigkeit Wert a bestimmen, damit f im Intervall auch noch stetig ist. Mathelounge
Eine Funktion f heißt stetig, wenn sie an jeder Stelle ihres Definitionsbereiches stetig ist. Hier ist nur nach der Stetigkeit an einem Punkt gefragt. Also musst du prüfen, ob der Grenzwert x gegen 2 der Normalparabel gleich dem Funktionswert an dieser Stelle ist.
Stetigkeit von Funktionen StudyHelp OnlineLernen
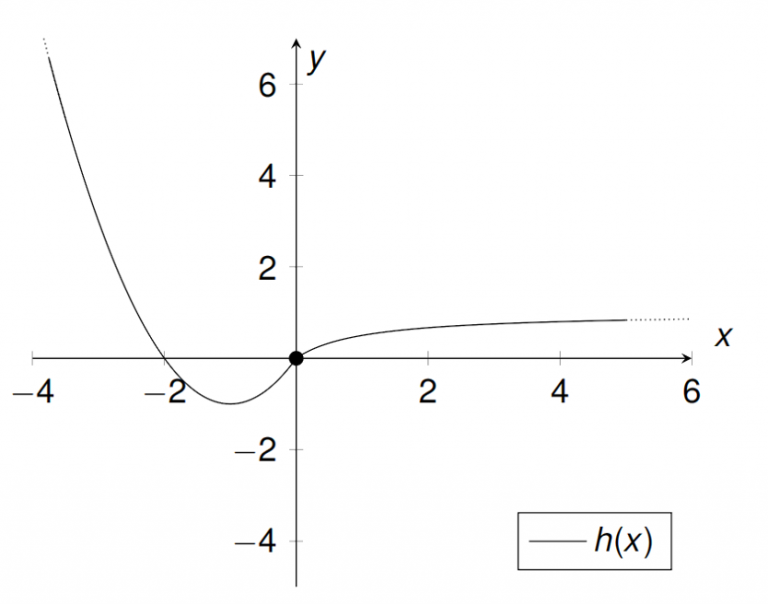
Stetigkeit. Mathematischer Grundbegriff. Eine Funktion f ist stetig an der Stelle x0 wenn gilt: limx→x−0 f(x) = lim x→x+0 f(x) = f(x0) Wenn also der linksseitige Grenzwert der Funktion (an der Stelle x0) gleich dem rechtsseitigen Grenzwert der Funktion (an der Stelle x0) gleich dem Funktionswert ist (an der Stelle x0 ).
Stetigkeit und Differenzierbarkeit im Schaubild erklärt Mathe by Daniel Jung YouTube

Die Stetigkeit einer Funktion kann von der Wahl des Definitionsbereichs abhängen. So gilt für die Einschränkungen Heaviside-Funktion und sind stetig. ist nicht stetig. ist in 0 rechtseitig stetig. Für Intervalle nennt man eine Funktion stetig auf, wenn ihre Einschränkung stetig ist. In diesem Sinne ist die Heaviside-Funktion stetig auf .
Verteilungsfunktion für stetige Wahrscheinlichkeitsverteilungen in einem Diagramm darstellen

Man spricht von einer stetigen Funktion, wenn die Funktion in jedem Punkt ihres Definitionsbereiches stetig ist. Beispiele stetiger und unstetiger Funktionen. Ist eine Funktion an einer Stelle differenzierbar, so ist sie dort auch stetig. Damit folgt insbesondere die Stetigkeit
WIKI Ableitungen Differenzierbarkeit Stetigkeit Fit in Mathe
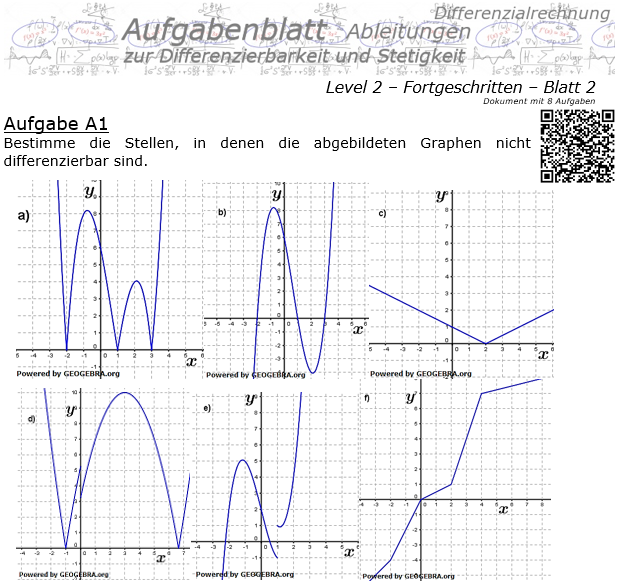
September 17, 2023. In diesem Artikel erklären wir, was stetige Funktionen sind und wie man ermittelt, ob eine Funktion an einem Punkt stetig ist oder nicht. Darüber hinaus finden Sie Eigenschaften stetiger Funktionen und Kontinuitätsanalysen der häufigsten Funktionen.